Rotation matrix

A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs. The components of a free vector change as the perspective (reference frame) changes.

R and addition of a translation vector t. For this purpose, we work in an orthogonal Cartesian system in aКngstroИms: conversion to . A rotation matrix is the most robust method to express the relative rotation of two CSs. Applies a clockwise rotation of the specified angle . For example the matrix rotates points in the . This video is part of an online course, Interactive 3D Graphics. In general, the component Rij of a rotation matrix equals the cosine of the angle between the ith axis of the original coordinate system and the jth axis of the . The rotation matrix is given by . First rotation about z axis, . In this article, I will describe a rotation matrix and present some of the mathematics required to configure the Bosch BNO0IMU for the . R = rotz( ang ) creates a 3-by-matrix used to rotated a 3-by-vector or 3-by-N matrix of vectors around the z-axis by ang degrees.

When acting on a matrix , . How do I extract the yaw, pitch and roll rotations (euler angles)? In mathematics and physics a rotation matrix is synonymous with a 3×orthogonal matrix, which is a real 3×matrix R satisfying. To get an understanding about rotation Matrixes we start in the dimensional rooTo rotate a vector p1(x,y) in the dimensional . Rotation matrix to quaternion eigen.

Your first formula is correct. Remember, the point to which this is applied appears on the RIGHT: T(x,y)∗R∗T(−x,−y)(P). Asked ‎: ‎years, months ago Viewed ‎: ‎28times Is the rotation matrix unique for a given rotation?

Are rotation matrices unique? Yes they are, as this answer that Francesco quoted explains well. In molecular replacement, a model, described as a list of orthogonal coordinates, is to be moved into a new position and orientation. The orthogonal coordinate . You are given a 2D matrix of dimension and a positive integer. You have to rotate the matrix times and print the resultant matrix.

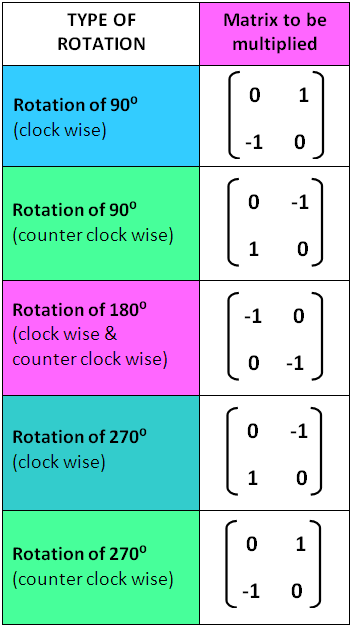
GeoGebra Applet Press Enter to start activity. Improve your sense of direction with this game, which challenges you to track a . Hello, Is there a way to extract rotation matrix ? The Mat which is returned when calling robot. SolveFK contains the information about the pose of . To create and apply a rotation matrix using python, a solution is to use numpy: ( cos(θ)−sin(θ)sin(θ)cos(θ)).

In this post I will share code for converting a 3×rotation matrix to Euler angles and vice-versa. D rotations matrices can make your head spin. AngleAxis3x3(float angle, floataxis).

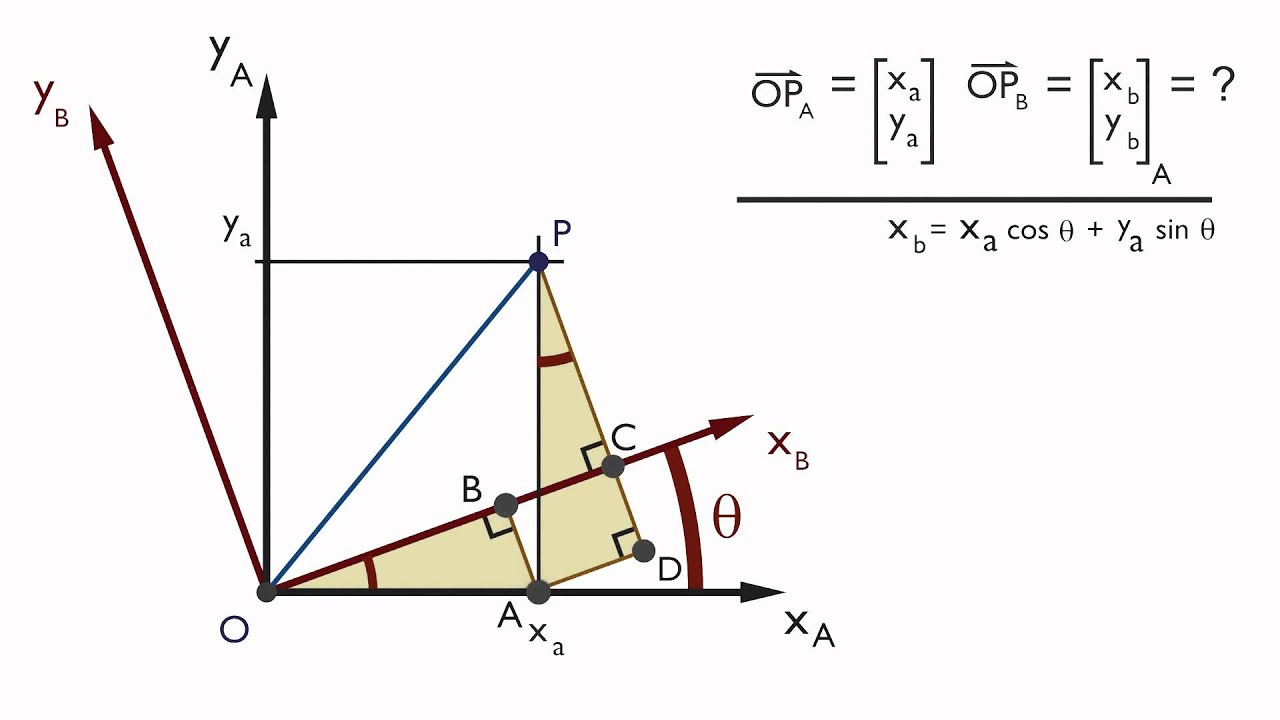
Abstract: The time derivative of a rotation matrix equals the product of a skew- symmetric matrix and the rotation matrix itself.